Bivariate Statistical Functions, Conditional Distributions
This post shows an example of a bivariate density function and its related distribution functions, conditional distribution- and conditional density functions. The examples are taken from here, plots are added. Hopefully, this post will shed some light onto the properties and characteristics of bivariate conditional functions, both density and distribution functions.
Density Function
A bivariate density function is given as
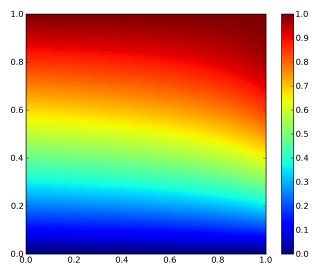
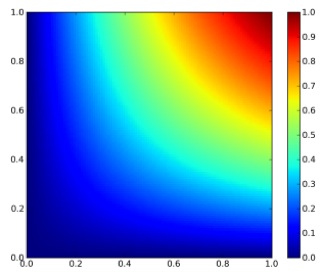
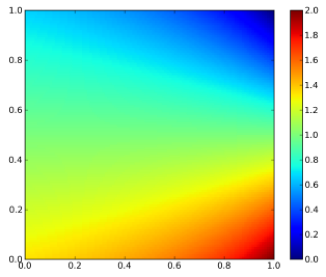
$$ f_{X,Y}(x,y) = \begin{cases} 2-x-y & 0 The plot of the bivariate density is shown on Figure 1. Figure 1: Bivariate density function By integrating twice (for each variable), the bivariate distribution function is obtained: $$ F_{X,Y}(x,y) = 2xy – \frac{1}{2}x^{2}y – \frac{1}{2}xy^{2} $$ The plot of the bivariate distribution function is shown on Figure 2. Figure 2: Bivariate distribution function The conditional density function is given generally by $$ f_{X|Y}(x|y) = \frac{f_{X,Y}(x,y)}{f_{Y}(y)} $$ and $$ f_{Y|X}(y|x) = \frac{f_{X,Y}(x,y)}{f_{X}(x)} $$. The marginal distributions of X and Y are given as $$ f_{X}(x) = \sum_{y \in D(Y)} f_{X,Y}(x,y) $$ and $$ f_{Y}(y) = \sum_{x \in D(X)} f_{X,Y}(x,y) $$ For the given density function, $$ f_{Y|X}(y|x) = \frac{2-x-y}{3/2-x} $$. The contour plot of this equation is shown on Figure 3. Note that this is not identical to the conditional on y! If x is really small and just bigger than 0 then there are medium range probabilities for y to be anything between 0 and 1. If x is really big and close to 1, then the probability is much higher that y is small than that y is big. Figure 3: Conditional density of y on x. The conditional distribution function for our example for $$ 0 $$ F_{Y|X}(y|x)=\frac{(2-x)y – 1/2y^{2}}{3/2-x} $$ the contour plot of which is shown on Figure 4. The conditional distribution function is the bivariate density function integrated along one direction, devided by the marginal density of the variable that it is conditioned on (not the one along which the bivariate density is integrated along). At first glance this seems odd, cause there is a density function (the marginal density) in the expression for a distribution function. But this density is independent of the variable along which is integrated! Figure 4: Conditional distribution function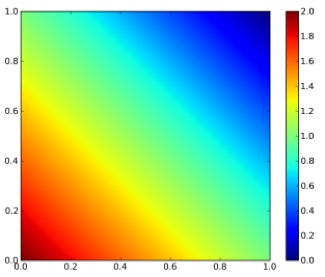
Distribution Function
Conditional Density Function
Conditional Distribution Function