Archive for October, 2010
Recent Readings
Here are some links I recently came across, which might be relevant to the grand theme of this blog: 🙂
- The AGU has started to host an “uber-blog“: it includes seven blogs by independent geo-scientists and three blogs by AGU staff on AGU meetings, on science communication, and general AGU sciences;
- Daniel Stellar at the Columbia Water Center wrote on the relationship between water quantity and quality;
The journal “Foreign Policy” published an article on the role of China, other Asian states, and the USA in the Mekong River basin;
[foreign secretary] Clinton recently met with the foreign ministers of Cambodia, Laos, Thailand, and Vietnam and pledged $187 million to support the Lower Mekong Initiative, which has the stated aim of improving education, health, infrastructure, and the environment in the region.
- Anne Jefferson, wrote on “Highly Allochthonous” how she uses rock samples to teach students on porosity and effective parameters;
- The Telegraph reports that “Scientists create dry water” — and see use of it to increase safety of potentially harmful liquids during transport;
- Peter Gleick: “The Human Right to Water, at Last“;
- Finally, the Scientific Fundamentalist write about “]Why Intelligent People Drink More Alcohol][9]”;
R.I.P. Benoît Mandelbrot
Here are his orbituaries at Wired and at the NY Times.
update Saturday; October 23, 2010:
More on Mandelbrot’s work and “his set” at the Wolfram Blog
Identi.ca Weekly Updates for 2010-10-20
- nice example of #calculating #probabilities based on possibilities: summer births ? more boy births? http://ke-we.net/5tf #
- "when construction costs runneth over": irrational optimism planning major building projects #rail #tunnel NJ-NY #s21 http://ke-we.net/5tb #
Identi.ca Weekly Updates for 2010-10-13
- Blog Action Day 2010 on Friday, Oct. 15th!: #clean #water to drink for everyone! #BAD2010 @blogactionday #
October 15th – Blog Action Day
This is a quick notice, that this coming friday, October 15th, is Blog Action Day!
Each year bloggers from more than 100 countries come together and blog about a single important issue, and this year’s topic is clean water. There is a petition to the UN on supplying clean drinking water to everybody.
For more, please check back on October 15th!
Random Numbers
The importance of random numbers is often overlooked. Even the people who should realize their importance take their existence for granted. Uniform random numbers are a function and then they are generated. Ok, the ones in Excel are not the greatest. The typical ones in programming languages are ok. Some people have their special random numbers.
There are a few interesting ways to generate random numbers: My favourite to date was the lava lamp random generator, whose current version can be found online here and doesn’t require an actual lava lamp anymore.

A lava lamp could be the source for random numbers
I just found out about a novel approach. Christian Gabriel at the Institute for Optics, Information and Photonics at the University of Erlangen, Germany recently published a novel method to generate random numbers: He proposed to
use vacuum fluctuations as quantum dice. Such fluctuations are another characteristic of the quantum world: there is nothing that does not exist there. Even in absolute darkness, the energy of a half photon is available and, although it remains invisible, it leaves tracks that are detectable in sophisticated measurements: these tracks take the form of quantum noise. This completely random noise only arises when the physicists look for it, that is, when they carry out a measurement. [from here]
The institute’s webpage states only that
By appropriately post-processing the measured data, truly random numbers which are solely based on quantum noise can be extracted.
I guess I would have to read the paper in detail what role the gaussian distribution plays and how the post-processing works exactly. In any way, this sure sounds like an interesting approach!
Bivariate Statistical Functions, Conditional Distributions
This post shows an example of a bivariate density function and its related distribution functions, conditional distribution- and conditional density functions. The examples are taken from here, plots are added. Hopefully, this post will shed some light onto the properties and characteristics of bivariate conditional functions, both density and distribution functions.
Density Function
A bivariate density function is given as
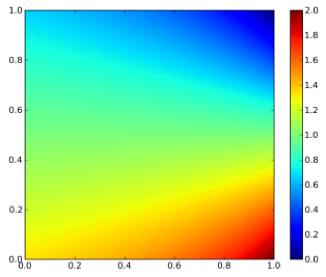
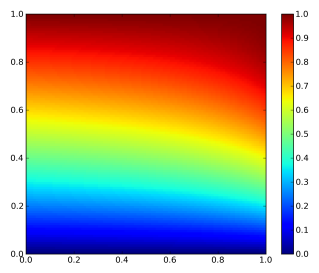
$$ f_{X,Y}(x,y) = \begin{cases} 2-x-y & 0 The plot of the bivariate density is shown on Figure 1. Figure 1: Bivariate density function By integrating twice (for each variable), the bivariate distribution function is obtained: $$ F_{X,Y}(x,y) = 2xy – \frac{1}{2}x^{2}y – \frac{1}{2}xy^{2} $$ The plot of the bivariate distribution function is shown on Figure 2. Figure 2: Bivariate distribution function The conditional density function is given generally by $$ f_{X|Y}(x|y) = \frac{f_{X,Y}(x,y)}{f_{Y}(y)} $$ and $$ f_{Y|X}(y|x) = \frac{f_{X,Y}(x,y)}{f_{X}(x)} $$. The marginal distributions of X and Y are given as $$ f_{X}(x) = \sum_{y \in D(Y)} f_{X,Y}(x,y) $$ and $$ f_{Y}(y) = \sum_{x \in D(X)} f_{X,Y}(x,y) $$ For the given density function, $$ f_{Y|X}(y|x) = \frac{2-x-y}{3/2-x} $$. The contour plot of this equation is shown on Figure 3. Note that this is not identical to the conditional on y! If x is really small and just bigger than 0 then there are medium range probabilities for y to be anything between 0 and 1. If x is really big and close to 1, then the probability is much higher that y is small than that y is big. Figure 3: Conditional density of y on x. The conditional distribution function for our example for $$ 0 $$ F_{Y|X}(y|x)=\frac{(2-x)y – 1/2y^{2}}{3/2-x} $$ the contour plot of which is shown on Figure 4. The conditional distribution function is the bivariate density function integrated along one direction, devided by the marginal density of the variable that it is conditioned on (not the one along which the bivariate density is integrated along). At first glance this seems odd, cause there is a density function (the marginal density) in the expression for a distribution function. But this density is independent of the variable along which is integrated! Figure 4: Conditional distribution function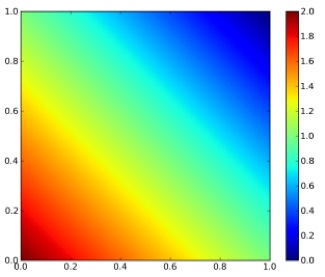
Distribution Function
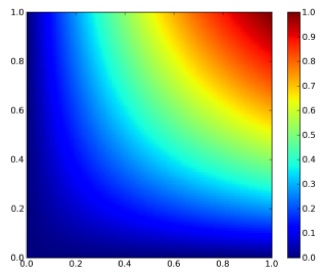
Conditional Density Function
Conditional Distribution Function
Identi.ca Weekly Updates for 2010-10-06
- October 15th: Blog Action Day 2010 – #Water http://blogactionday.change.org/ #
- nice pictures: CIWM #environmental #photographers of the year: winners announced: http://ke-we.net/4p7 #
Die Zukunft des Wassers
In his book “Die Zukunft des Wassers: Eine Reise um unsere Welt”, Erik Orsenna presents the current state of the water related issues around the world by a series of short stories which are focused on a certain area of the world. Each of these stories, are compact and independently readable from the other stories, however they are nicely linked.
The book is very well translated, the original is French, which is one factor that leads to its great readability. Even though, I spotted one mistake at the end which is sort of sad for this book with its topic: “viaduct” was used instead of “aqueduct”. The other factor that enhances the book’s readability and authenticity is the knowledge about water-issues that Orsenna gained while travelling the world for two years and researching water problems. This knowledge is laid out in plain language, and the short stories are well understandable for everybody, no knowledge in water related topics is required. Some water-projects presented were new to me, for example the work that is underway in Singapore.

Erik Orsenna: Die Zukunft des Wassers
Later in the book, Orsenna touches on issues of water pricing, the discussion of water as a public or a private good, virtual water footprint at the end. The book closes with pointing out the importance of the agricultural sector — agriculture is the world’s biggest water user and polluter. Hence Orsenna proposes to start changing the behaviour of water use in this sector.
Geology-Moments, Math Education, Extreme Events
Important Geologic Experiences
Outside the Interzone publishes a series of blogposts where people are asked to contribute which are called “Accretionary Wedge” (a mass of sedimentary material scraped off a region of oceanic crust during subduction and piled up at the edge of the overriding plate). The 27th issue is on “Important Geological Experiences“. Most of them are hard-core geology-related.
There are two less core-geology posts:
- Cian Dawson (with his fairly new blog “Point Source“) wrote about his experiences with electrical resistivity surveys and about the associated “black box” inverse models. He comes up with the conclusion that “we must take the time to fully understand the tools we use, whether we’re talking about a compass in the field or software in the office“. Nicely put!
- Anne Jefferson at “Highly Allochthonous” writes about her affinity with floods (or vice vera) and shows some pictures of extensive flooding at an unlikely location: Alice Springs, Australia
Math (and other) Education
Jon McLoone at the Wolfram Blog wrote on math education. Using the example of calculating the range of a gun, he makes the point that our math education is missing reality. Typical problems in math education are over-simplified, and when computers are used together with those simple examples, there is nothing left to think about.
I am not sure if I agree. On the one hand I do, because I hated the style we were taught analysis in high school, which is cookbook style. We weren’t even told, what the first derivative of a function means, we simply had to calculate its coordinates. On the other hand, I think it’s simply important that you can calculate derivatives.
The example he comes up in a very structured step-by-step approach is indeed very much more realistic, and I can see how it can improve understanding of the subject. And I would argue if somebody who is learning analysis can code the problem like Jon in his example, even the “dumb model” he has gained quite decent understanding.
Which leaves the question of what computers, what programming language should be taught? Does it matter at all? Just any? At which point in the education? In my teaching experience I am faced with 3rd year engineers who have never used Excel.
Extremes Seem to Have Become the Norm
Andrew Revkin writes about “Weird Weather in a Warming World“. There have been many “extreme” floods this summer, in the US, in Pakistan, and currently in Germany (amongst many others, I’m sure). These observations can quickly lead to the conclusion that the return period for a given intensity shrinks and shrinks, possibly due to climate change. However, Andrew points out, there is no evidence for this conclusion (yet).
However, he points out (in a blog post at dotearth) that “the odds of extreme and prolonged heat or heavy rains will rise with an unabated buildup of warming emissions.“