Estimate the Distribution of an Underlying Process Based on Samples
Say you have many sets of samples (measurements). What do you do if you wanted to estimate the distribution of the underlying population? Ok, if all your samples are well behaving, you throw them in one pot, and estimate the distribution based on all the samples. Ok.
Now, what if you wanted, for whatever reason, to estimate the underlying distribution based on the individual sets of your samples? What you could do is estimate a distribution based on each sample. Then you would have to somehow average the distributions. How would you do that? By multiplication? Turns out – no. In fact, the average of the density functions of each sample seems to be a pretty good estimator of the underlying density function.
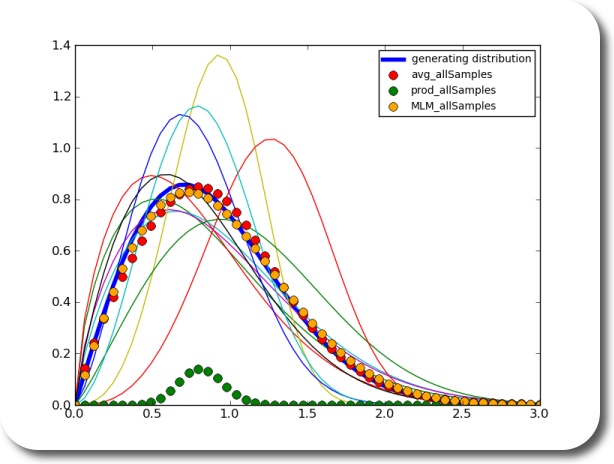
using 10 sets of samples with 10 samples each
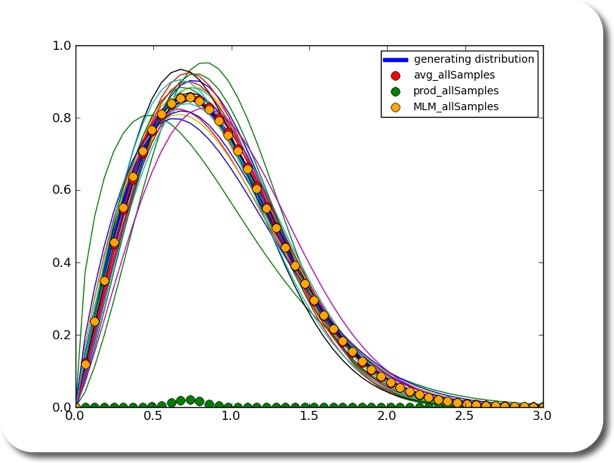
using 25 sets of samples with 100 samples each