Archive for November, 2012
New Books on Numpy, Pandas, Data Analysis
I became aware recently of three books that are related to data-analysis, modelling, and statistics in a fairly broad sense.
They are pictured below, from left to right:
- “Python for Data Analysis
” by Wes McKinney (of pandas fame) published by O’Reilly
- “NumPy Cookbook
” by Ivan Idris published by Packt Publishing
- “NumPy 1.5 Beginner’s Guide
” by Ivan Idris published by Packt Publishing

Python for Data Analysis
This is the most in-depth book. It covered the most important python modules: iPython, NumPy, Pandas, Matplotlib. Additionally, it has chapters containing examples on practical issues with data (aggregation, data with a time-stamp, sorting). I really just started diving into it. However, it already led me to upgrade to iPython 13.1. It seems like it is well suited for my level of understanding of programming: Having some experience, trying to learn more existing tools
NumPy Cookbook
The title already gives it away: The book is organised in sections with “recipes”. Mostly, these recipes are self-containing. The focus is clearly on NumPy, even though Matplotlib, iPython, and also Pandas are covered to some extent. I enjoyed browsing through it, most of the examples are interesting (resizing images, playing with PythonAnywhere (like I’ve done before), f.ex). Generally, I think this is a great resource to have.
NumPy 1.5
Despite being by the same author (Ivan Idris), there is positively little overlap between his two books. “NumPy 1.5” covered NumPy in great detail, and is as such mostly useful for beginners who try to use python for some numerical analysis. When I read this book, I also was reminded, that the webpage that lists NumPy functions is a very valuable resource (which I tend to spend too little time with).
It is interesting to see that people realise that there is a market for books explaining open source tools. And I do think those books complement available documentation nicely.
Pandas in Python: Use with Hydrological Time Series
I recently had some time series analysis to do, and I decided to do this work in Pandas. Particualarly, I had to deal with many timeseries, stretching from different startpoints in time to different endpoints in time. Each timeseries was available as an ASCII file. The data were daily data. The time information was given in three columns, each representing year, month, and day, respectively.

Image: http://flic.kr/p/9gK3ZH
I found these two posts by Randal S. Olson very useful resources:
- Using pandas DataFrames to process data from multiple replicate runs in Python (link)
- Statistical analysis made easy in Python with SciPy and pandas DataFrames (link)
Here is a cookbook style layout of what I did:
The following steps show how easy it was to deal with the data 1. Read the input data
cur_sim_ts = pa.io.parsers.read_table(os.path.join(data_path, 'test', result)
, header=None
, sep='\s*'
, parse_dates=[[0,1, 2070]]
, names=['year','month', 'day', result[:-4]]
, index_col=[0]
)
where `’\s*’ means any whitespace. The dates were given in three colums, one for year, month, and day. Can it get simpler and nicer than that?
It is possible to repeat 1 multiple time, each time extending the pandas data_frame. Unfortunately, this looks a little ugly still, but works
if counter_cur_file > 0: final_df = final_df.combine_first(cur_sim_ts) else: final_df = cur_sim_ts.copy() / 10.0In the else part, the Pandas data_frame is initialised. It so happens that this and only this series of the loop has to be divided by ten. In all other cases the time_series that was read in step 1 is “appended” (or rather combined with) the the previously initialized data_frame. The wicked thing is that each time_series is put at the propper “place” in time within the data_frame. Dates are real dates. This is beautiful, but I had to be a little carfule with the data I had at hand, in which every month has 30 days.
As soon as this data_frame is constructed, things are easy, for example
plotting, particularly plotting only a certain time-interval of the data.
final_df['2070-01-01':'2100-12-30'].plot(ylim=[-10,45])saving the data_frame
final_df.save(os.path.join(out_path, pickle_filename))
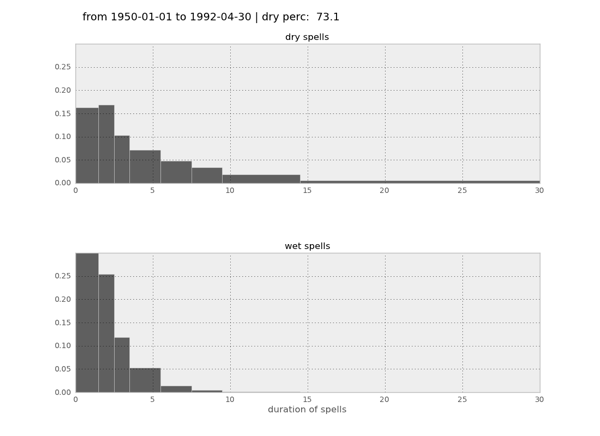
For me it was of particular interest to find out, how many consecutive dry and wet days there are in each time series. I introduced a threshold of precipitation. If the daily amount of precipitation is above that threshold, this day is considered to be “wet”, else it’s considered to be “dry”. I wanted to count the number of consecutive dry and wet days, and remember them for a time series. This is the purpose of the function below. It is coded a little bute force. Still I was surprised, that it performed reasonably well. If anybody has a better idea, please let me know. Maybe it can be of use for other Pandas users. Note: a time_series in the Pandas world is obtained by looping over a data_frame
def dry_wet_spells(ts, threshold): """ returns the duration of spells below and above threshold input ----- ts a pandas timeseries threshold threshold below and above which dates are counted output ------ ntot_ts total number of measurements in ts n_lt_threshold number of measurements below threshold storage_n_cons_days array that stores the lengths of sequences storage_n_cons_days[0] for dry days storage_n_cons_days[1] for wet days """ # total number in ts ntot_ts = ts[~ ts.isnull()].count() # number lt threshold n_lt_threshold = ts[ts <= threshold].count() # type_day = 0 # dry # type_day = 1 # wet # initialisierung: was ist der erste Tag type_prev_day = 0 storage_n_cons_days = [[],[]] n_cons_days = 0 for cur_day in ts[~ ts.isnull()]: # current day is dry if cur_day <= threshold: type_cur_day = 0 if type_cur_day == type_prev_day: n_cons_days += 1 else: storage_n_cons_days[1].append(n_cons_days) n_cons_days = 1 type_prev_day = type_cur_day else: type_cur_day = 1 if type_cur_day == type_prev_day: n_cons_days += 1 else: storage_n_cons_days[0].append(n_cons_days) n_cons_days = 1 type_prev_day = type_cur_day return ntot_ts, n_lt_threshold, storage_n_cons_days- With all of this, I can produce histograms like this: